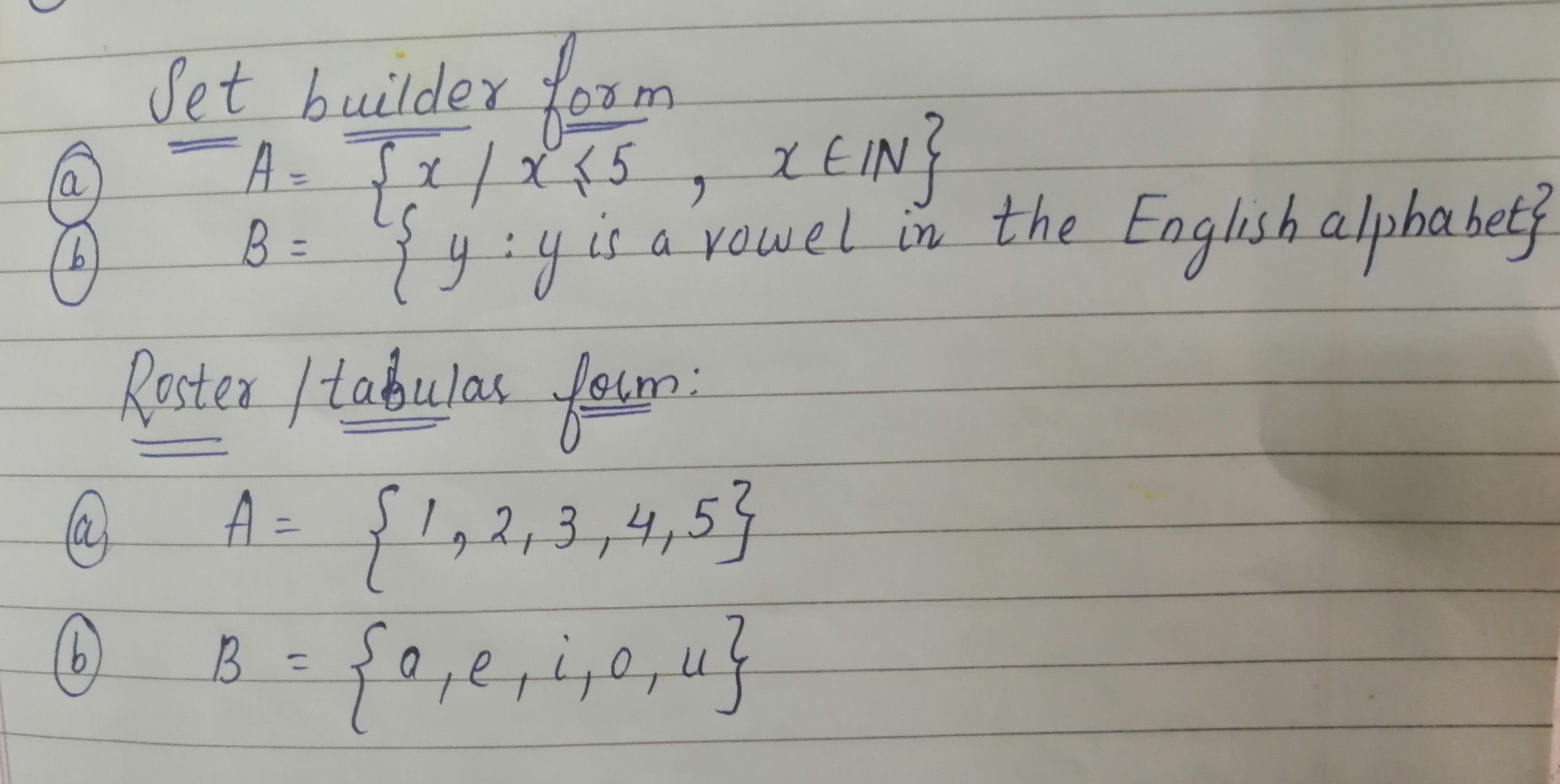Set Builder And Roster Method

There are mainly two methods that can be used to represent a set. The Listing method is also called the roster method. This method shows the list of all the elements of a set inside brackets. The elements are written only once and are separated by commas. The set builder notation includes one or more than one variable. It also defines a rule about the elements which do not belong to the set and which elements belong to the set.

Let us read about different methods of writing sets. For example, the number 5 is an integer, and so it is appropriate to write \(5 \in \mathbb\). It is not appropriate, however, to write \(5 \subseteq \mathbb\) since 5 is not a set. It is important to distinguish between 5 and .

The difference is that 5 is an integer and is a set consisting of one element. Consequently, it is appropriate to write \(\ \subseteq \mathbb\), but it is not appropriate to write \(\ \in \mathbb\). The distinction between these two symbols is important when we discuss what is called the power set of a given set.

The roster notation is a simple mathematical representation of a set in mathematical form. In this method, the elements are enumerated in a row inside the curly brackets. If the set contains more than one element, then every two elements are separated by a comma symbol. Therefore, set builder notation is a method of writing sets often with an infinite number of elements. It is commonly used with rational numbers, real numbers, complex numbers, natural numbers, and many more. This notation can also be used to express sets with intervals and equations.

Learning to write sets in roster form means listing elements, separated by commas, inside a group of braces. Study a few limitations of this method, the ways to apply it accurately, and the formulas that dictate its use. Set Builder Notations is the method to describe the set while describing the properties and not just listing its elements. When there is set formation in a set builder notation then it is called comprehension, set an intention, and set abstraction. In Preview Activity \(\PageIndex\), we worked with verbal and symbolic definitions of set operations. However, it is also helpful to have a visual representation of sets.

Venn diagrams are used to represent sets by circles drawn inside a rectangle. The points inside the rectangle represent the universal set \(U\), and the elements of a set are represented by the points inside the circle that represents the set. For example, Figure \(\PageIndex\) is a Venn diagram showing two sets. In roster form, all the elements of the set are listed, separated by commas and enclosed between curly braces .

But the problem arises when we have to list elements lying inside either the small intervals or a very large set of numbers, or even an infinite set. Using roster notation does not make sense and is a very tedious method. Therefore, we use set-builder notation for such conditions.

Set-builder notation is a representation used to write sets, often for sets with an infinite number of elements. It is used with common types of numbers, such as integers, real numbers, and natural numbers. This notation can also be used to express sets with an interval or an equation.

Let \(A\) and \(B\) be subsets of a universal set \(U\). For each of the following, draw a Venn diagram for two sets and shade the region that represent the specified set. In addition, describe the set using set builder notation.

There are several ways on how to write a number. One of these methods is the set builder notation, with the others being interval notation and roster notation. Set builder notation is defined as a mathematical notation used to describe a set using symbols. It is used to explain elements of sets, relationships, and operations among the sets.

A collection of numbers, elements that are unique can be described as a set. In this article, we learned about sets, properties of sets, and elements of a set. Then we learned about the three methods to represent a set- Description Method, Roster or Tabular Method, and Rule or Set-Builder Method. In addition to this, we learned to convert the roster form to set-builder form and vice versa. Furthermore, we learnt the cardinality of a set.

The objects that are used to form a set are called its elements or its members. In general, the elements of a set are written inside the curly braces and separated by commas. The name of the set is always written in capital letters. Set-builder notation comes in handy to write sets, especially for sets with an infinite number of elements. Numbers such as integers, real numbers, and natural numbers can be expressed using set-builder notation.

A set with an interval or an equation can also be expressed using this method. In this, a rule, or the formula or the statement is written within the pair of brackets so that the set is well defined. In the set builder form, all the elements of the set, must possess a single property to become the member of that set.

This is best used to represent the sets mainly with an infinite number of elements. It is used commonly with integers, real numbers, and natural numbers. This also is used to represent the sets with intervals and equations. Students have to be very clear and learn precisely so that they can solve any problem related to the topic. Students can refer to Vedantu and learn the chapter clearly with a detailed explanation of every topic.

The method of defining a set by describing its properties rather than listing its elements is known as set builder notation. Set builder notation contains one or two variables and also defines which elements belong to the set and the elements which do not belong to the set. The rule and the variables are separated by slash and colon.

This is often used for describing infinite sets. Use set builder notation or the roster method to specify the set of integers that are the sum of eight consecutive integers. Use set builder notation or the roster method to specify the set of integers that are the sum of four consecutive integers. Mathematical sets are collections of objects or concepts that can be joined together to become mathematical building blocks. Learn about mathematical sets and understand their function in mathematics. Explore the roles of elements, intersections, and unions in mathematical sets.

Observing the relationships between the set elements and writing the condition as a statement to change from roster form to set builder form. The roster method is defined as a way to show the elements of a set by listing the elements inside of brackets. An example of the roster method is to write the set of numbers from 1 to 10 as . An example of the roster method is to write the seasons as . A set is a collection of well-defined objects. These objects may be actually listed or may be specified by a rule.

In this article, we shall study the application of the definition of a set. Similarly, we shall study to write sets by roster method and set-builder method. In Python, the set-builder's braces are replaced with square brackets, parentheses, or curly braces, giving list, generator, and set objects, respectively. Haskell replaces the set-builder's braces with square brackets and uses symbols, including the standard set-builder vertical bar. In this case, the description of the common property of the elements of a set is written inside the braces.

This is the simple form of a set-builder form or rule method. Set is a well-defined collection of objects or elements. A Set is represented using the Capital Letters and the elements are enclosed within curly braces . Refer to the entire article to know about Representation of Set in three different ways such as Statement Form, Set Builder Form, Roster Form.

For a Complete idea on this refer to theSet Theoryand clear all your queries. Check out Solved Examples for all three forms explained step by step. We need to use set builder notation for the set \(\mathbb\) of all rational numbers, which consists of quotients of integers. Before beginning this section, it would be a good idea to review sets and set notation, including the roster method and set builder notation, in Section 2.3. Set notation is used to define the elements and properties of sets using symbols.

Symbols save you space when writing and describing sets. Set notation also helps us to describe different relationships between two or more sets using symbols. Moreover, learn to understand the common symbols used in set notation and learn how to write set notation from set notation examples. Discover the subset definition and analyze subset examples for both categorical and mathematics subsets using subset notation.

Set builder notation is a mathematical notation that describes a set by stating all the properties that the elements in the set must satisfy. It is specifically helpful in explaining the sets containing an infinite number of elements. The elements of a set are written inside a pair of curly braces and separated by commas.

You can list all even numbers between 10 and 20 inside curly braces separated by a comma. Here we are going to see examples on roster form and set builder form. The Interval notation is a method to define a set of numbers between a lower limit and an upper limit by using end-point values.

The point also has to be remembered that the upper and lower limits may or may not be included in the set. A square bracket denotes inclusion in the set, while the brackets indicate exclusion from the set. In set theory, the power set of a Set A is defined as the set of all subsets of the Set A including the Set itself and the null or empty set. The set builder notation is very important as, in writing down many sets, where the roster method cannot be used. The term used 'clever students in your class' is a relative term and choice may vary from person to person. Hence it is not a collection of well-defined objects.

Read the the power set definition and see how power set notation works. See a power set example to learn how to identify the elements in a power set. The Roster Method makes set notation a straightforward concept to comprehend. But this method lacks universality and accuracy as all sets can not be defined using this method as enumeration can be too long or difficult to be explained.

Therefore, some sets require to be defined by the properties that illustrate and describe their elements. Is a list of all of the elements in a set, separated by commas, and surrounded by French curly braces. In this method, a well-defined description of the elements of a set is made. At times, the definition of elements is enclosed within the curly brackets.

Listing the elements of a set inside a pair of braces is called the Roster Form. On the other hand, in Set Builder Form, the statement is enclosed within brackets, which allows for a better definition of the set. All elements of a set must possess the same property in the Set Builder form to become a member of that set.

In this article, we will have a detailed discussion about the Roster Form and Set Builder Form. We can write the domain of f in set builder notation as, . If the domain of a function is all real numbers we can state the domain as, 'all real numbers,'. Also, we can use the symbol to represent all real numbers.

A set-builder notation describes the elements of a set instead of listing the elements. We read the set as the set of all x such that x is a number greater than 4 and less than 10. Listing the elements of a set inside a pair of braces is called the roster form. In Mathematics, the set is an unordered group of elements represented by the sequence of elements between curly braces . In Preview Activity \(\PageIndex\), we learned how to use Venn diagrams as a visual representation for sets, set operations, and set relationships.

Roster Method And Set Builder Notation Examples In that preview activity, we restricted ourselves to using two sets. We can, of course, include more than two sets in a Venn diagram. Figure \(\PageIndex\) shows a general Venn diagram for three sets (including a shaded region that corresponds to \(A \cap C\)). If you are asked to list a set of integers between 1 and 6, inclusive, then you can simply use a roaster form to write .

How To Download Windows 11 On Windows 10

If your existing Windows 10 PC is running Windows 10 20H1 or later and meets the minimum hardware specificationsit will be able to upgrade to Windows 11. The upgrade rollout plan is still being finalized, but for most devices already in use today, we expect it to be ready sometime in early 2022. Not all Windows 10 PCs that are eligible to upgrade will be offered to upgrade at the same time. To see if your PC is eligible to upgrade, refer to our knowledge base for a list of tested systems. Once the upgrade rollout has started, you can check if it is ready for your device by going to Settings/Windows Updates.

More information on how that is presented will be available at a later date. Additional desktop notification options may be also be added at a later date. Original equipment manufacturers can still ship computers without a TPM 2.0 coprocessor upon Microsoft's approval. Some third-party software may refuse to run on unsupported configurations of Windows 11. On Windows 11 , a clean installation refers to the process of erasing the hard drive and applying a fresh copy of the OS without custom settings, drivers, apps, or files. Typically, this is the recommended approach to upgrade to the latest version of Windows 11 on compatible hardware to prevent installation issues and fix existing problems.

Using the same approach as in previous versions with Machine Learning and Artificial Intelligence technologies, Microsoft will begin the gradual and very slow rollout on Windows 11 on Oct. 5. Initially, the deployment will start with newer devices that meet the minimum hardware requirements and have a good upgrade experience. Also, on this day, retailers and computer companies (Dell, HP, ASUS, Acer, etc.) will begin shipping many of their new laptops and desktops with Windows 11 pre-installed.

He also acknowledged the expansion of Microsoft Store to include more "traditional" desktop applications. Citing security considerations, the system requirements for Windows 11 were increased over Windows 10. While the OS can be installed on unsupported processors, Microsoft does not guarantee the availability of updates.

Windows 11 also drops support for 32-bit x86 CPUs and devices which use BIOS firmware. The option is available to reinstall Windows 11 when the local image is not working, or you do not want to use the same installation settings provided by the manufacturer. If you select the "Cloud download" option, the feature will download the same version already installed on the computer, which means you cannot use this method to upgrade to a newer version.

Also, if the device was using a custom image from the manufacturer, the new installation won't include the custom settings, drivers, or tools. Microsoft supports multiple ways to clean install Windows 11, including using a USB flash drive to set up the OS on an SSD (Solid-State Drive). It's also possible to use the "Reset this PC" feature to quickly wipe out the hard drive and reinstall the OS without additional tools. Or, if the device does not start, you can use the Advanced startup options or mount the ISO file to File Explorer to start a clean install. If your existing Windows 10 PC is running the most current version of Windows 10 and meets the minimum hardware specifications it will be able to upgrade to Windows 11. Not all Windows 10 PCs that are eligible to upgrade to Windows 11 will be offered to upgrade at the same time.

Actually installing Windows 11 is a very simple process. Once you have created installation media, you can simply launch the setup file in your flash drive, then click through the installing process. Once the installation process is finished, you'll be running Windows 11. If you want to do it this way, it's pretty much the same as having an ISO file.

As part of the minimum system requirements, Windows 11 only runs on devices with a Trusted Platform Module 2.0 security coprocessor. According to Microsoft, the TPM 2.0 coprocessor is a "critical building block" for protection against firmware and hardware attacks. In addition, Microsoft now requires devices with Windows 11 to include virtualization-based security , hypervisor-protected code integrity , and Secure Boot built-in and enabled by default. The operating system also features hardware-enforced stack protection for supported Intel and AMD processors for protection against zero-day exploits.

The only difference is that the feature will download the installation files from the Microsoft server. For example, if the computer had the same setup for a long time, a clean install of Windows 11 can help resolve performance issues, problems shutting down, booting up, memory, and apps. Also, this type of installation is the best method to upgrade from an older version, such as Windows 7 or Windows 8.1.

In addition, you can use this option to delete annoying bloatware that came preloaded with the default setup. After the tool becomes available, you can download it from this Microsoft support website by clicking the Download Now button under the "Create Windows 11 Installation Media" section. Then, you can launch the Media Creation Tool, use the USB flash drive option, and continue with the on-screen directions to create the installation media. First make sure you have a full backup of your data since will be installing on top of the existing data.

You can download the Windows 10 media from the Windows 10 .iso download site and then set the computer to boot from the flash drive. Typically, I find this is often the hardest part of the process — finding the combination of keys that allows you into the bios to force the system to boot from the flash drive. What you need is a Windows 11 ISO file you can boot from and use for a clean install or an in-place upgrade. First, you can download a Windows 11 ISO directly from Microsoft.

Finally, you can use Aveyo's open-source Universal MediaCreationTool to create an ISO that bypasses WIndows 11's TPM requirement. It's not imperative that you upgrade your system to Windows in the next couple of weeks, or even months. For many people, that's about the time to upgrade to a newer device, one that will come with Windows 11 already installed.

Starting with the release of Windows 11, the Media Creation Tool no longer includes an option to perform a clean installation or in-place upgrade. You can only use the tool to create a bootable media to perform an installation using a USB flash drive or ISO file. Once you complete the steps, the recovery feature will continue with the reinstallation using the locally available image of Windows 11.

If you have a computer from HP, Dell, Acer, or another brand, this process will restore the original settings. This means the factory settings, drivers, applications, and tools the manufacturer included in the custom image. After you've prepared your PC for installation, you'll want to back up Windows 10. While there isn't a hard-and-fast rule, it's highly recommended to have an external hard drive with at least 500GB worth of space or have a cloud-based solution available. Each has its pros and cons, so consider that when backing up your files. While backing up your data is good practice in general, this is especially important when installing a large update/new OS if something goes wrong during the installation process.

As I've noted in past blogs, being on the latest version of Windows provides you with the best in creativity, protection and productivity. This has never been truer than with Windows 11! Windows 11's minimum system requirements enable a new era of experiences, reliability and security.

AsPanos Panay shared in June, this is the first version of a new era of Windows. And, for customers who are using a device that is not eligible for Windows 11, Windows 10 is a great place to be. Devices that do not meet the minimum system requirements will remain on Windows 10 and continue to be supported with security updates.

Customers using long term service releases will continue to be supported through the published end of support dates. For more information about Windows 10 support, see HP products tested with Windows 10. At least 16GB of RAM The basic system requirements of Windows 11 differ significantly from Windows 10. Windows 11 only supports 64-bit systems such as those using an x86-64 or ARM64 processor; IA-32 processors are no longer supported. Thus, Windows 11 is the first ever consumer version of Windows not to support 32-bit processors and 16-bit software . The minimum RAM and storage requirements were also increased; Windows 11 now requires at least 4GB of RAM and 64GB of storage.

S mode is only supported for the Home edition of Windows 11. The compatibility list includes the Intel Core i7-7820HQ, a seventh-generation processor used by the Surface Studio 2, although only on devices that shipped with DCH-based drivers. Internet Explorer has been replaced by the Chromium-based Microsoft Edge as the default web browser, and Microsoft Teams is integrated into the Windows shell. Microsoft also announced plans to allow more flexibility in software that can be distributed via Microsoft Store, and to support Android apps on Windows 11 . After the download, double-click the ISO file and then double-click the setup.exe file.

Click Next at the initial install screen to check for and download any updates to Windows 11. At the Ready to Install screen, you will see that Windows 11 will be installed and personal files and apps will be kept by default. Another option is to create installation media on a USB key and install the operating system using that. A final option is to download a Windows 11 disk image to create a bootable installation media such as a USB stick or DVD, or create a virtual machine to install the new Windows software.

After your installation percentage has reached 100% and completed its processes, you're done! You will be presented with a new login screen to access your desktop. If you were upgrading from Windows 10, all of your files, programs, and desktop icons should be intact. If you notice anything is missing, you should find it safe on the backup you created at the beginning. The actual desktop will look different than Windows 10.

The Start menu is now centered and the Taskbar has a new frosted glass aesthetic for a fresh, modern look. If you followed the steps above, you might have been noticed that you can upgrade to Windows 11 If so, simply click Download and Install on the pretty banner at the top of the Update window. This process can take several hours depending on your internet connection and PC. When it's done, your system will prompt you to reboot the PC to continue with the installation process.

If you're running on a laptop, be sure to plug in your AC adapter now. Many games that use Anti-cheat tools also have started relying on Windows 11 security features to provide fair gameplay. While these games still work on Windows 10, it is only a matter of time before Windows 11 ends up becoming a requirement. Microsoft offers several ways to download Windows 11 manually. One is to use the Installation Assistant app, which you install on your PC to trigger a normal upgrade install via Windows Update.

The second is to use the Windows 11 Media Creation Tool, which automates the process of creating a bootable USB install drive or downloading an install ISO file. Once you have a USB drive, you can either boot from it to perform a clean install or run the Setup app from within Windows 10 to do a normal upgrade install. You can also burn the ISO to a DVD, but installing from any USB drive, even an old USB 2.0 drive, will be much faster, so you shouldn't do that. Finally, you can just download an ISO file directly from Microsoft's site. Once the installation is complete, you should find all of your files and applications in the same place you left them before the update. Some may sport a new look (those rounded edges on apps and folders look nice, don't they?) but everything should function as you remember.

Click Next to have Windows 11 check for any updates, then accept the license terms. The Ready to install screen shows that Windows 11 will be installed and that your personal files and apps will be kept. You can then elect to keep personal files and apps, personal files only, or nothing.

The recovery settings offer another method to start fresh with a clean copy of Windows 11. Unlike the Media Creation Tool, bootable flash drive, and ISO file options, you can only use this method to reinstall Windows 11 on a computer already running the same OS. All HUAWEI PCs with Windows 10 currently being sold on HUAWEI Consumer BG website will be able to upgrade to Windows 11.

For the PC to be able to upgrade to Windows 11, it must meet the minimum hardware specifications and specific hardware is required for some features. The upgrade rollout plan is still being finalized but is scheduled to begin late in 2021 and continue into 2022. Specific timing will vary by device and countries. There's a lot to enjoy in Windows 11, but remember that you're currently running an early version that isn't quite finished yet.

It's normal to experience some bugs or graphical glitches. For example, all of our custom Taskbar shortcuts were missing their icons after installation and needed to be re-pinned to appear again. Be sure to Check For Updates often as Microsoft releases bug fixes. If you experience a major problem, or just decide Windows 11 isn't for you, you can easily reinstall Windows 10 using Microsoft's Media Creation Tool to download a free installation file. If your hard drive is still MBR, then you'll need to format the boot drive as GPT.

Running the mbr2gpt commands will convert your boot drive without data loss, which is very handy. The process of running these commands is simple, so follow these steps to convert the hard drive. Also, be sure to watch Microsoft's in-depth tutorial video below for more detail. Please note that the Creator's Update must be installed first. You can refer to our knowledge base for a list of tested systems to determine if your device eligible to upgrade to Windows -11.

Many PCs that are less than four years old will be able to upgrade to Windows 11. They must be running 20H1 or later version of Windows 10 and meet the minimum hardware requirements to receive the Windows 11 upgrade. Upgrades to Windows 11 will begin to roll out late in 2021 and continue into 2022.

During this time, we will be doing some behind the scenes testing and validating for your specific PC. Windows Update will provide an indication if and when your PC is eligible. You can check to see by going to Settings/Windows Update. All Dell PCs with Windows 10 currently being sold on dell.com will be able to upgrade to Windows 11.