There are mainly two methods that can be used to represent a set. The Listing method is also called the roster method. This method shows the list of all the elements of a set inside brackets. The elements are written only once and are separated by commas. The set builder notation includes one or more than one variable. It also defines a rule about the elements which do not belong to the set and which elements belong to the set.
Let us read about different methods of writing sets. For example, the number 5 is an integer, and so it is appropriate to write \(5 \in \mathbb\). It is not appropriate, however, to write \(5 \subseteq \mathbb\) since 5 is not a set. It is important to distinguish between 5 and .
The difference is that 5 is an integer and is a set consisting of one element. Consequently, it is appropriate to write \(\ \subseteq \mathbb\), but it is not appropriate to write \(\ \in \mathbb\). The distinction between these two symbols is important when we discuss what is called the power set of a given set.
The roster notation is a simple mathematical representation of a set in mathematical form. In this method, the elements are enumerated in a row inside the curly brackets. If the set contains more than one element, then every two elements are separated by a comma symbol. Therefore, set builder notation is a method of writing sets often with an infinite number of elements. It is commonly used with rational numbers, real numbers, complex numbers, natural numbers, and many more. This notation can also be used to express sets with intervals and equations.
Learning to write sets in roster form means listing elements, separated by commas, inside a group of braces. Study a few limitations of this method, the ways to apply it accurately, and the formulas that dictate its use. Set Builder Notations is the method to describe the set while describing the properties and not just listing its elements. When there is set formation in a set builder notation then it is called comprehension, set an intention, and set abstraction. In Preview Activity \(\PageIndex\), we worked with verbal and symbolic definitions of set operations. However, it is also helpful to have a visual representation of sets.
Venn diagrams are used to represent sets by circles drawn inside a rectangle. The points inside the rectangle represent the universal set \(U\), and the elements of a set are represented by the points inside the circle that represents the set. For example, Figure \(\PageIndex\) is a Venn diagram showing two sets. In roster form, all the elements of the set are listed, separated by commas and enclosed between curly braces .
But the problem arises when we have to list elements lying inside either the small intervals or a very large set of numbers, or even an infinite set. Using roster notation does not make sense and is a very tedious method. Therefore, we use set-builder notation for such conditions.
Set-builder notation is a representation used to write sets, often for sets with an infinite number of elements. It is used with common types of numbers, such as integers, real numbers, and natural numbers. This notation can also be used to express sets with an interval or an equation.
Let \(A\) and \(B\) be subsets of a universal set \(U\). For each of the following, draw a Venn diagram for two sets and shade the region that represent the specified set. In addition, describe the set using set builder notation.
There are several ways on how to write a number. One of these methods is the set builder notation, with the others being interval notation and roster notation. Set builder notation is defined as a mathematical notation used to describe a set using symbols. It is used to explain elements of sets, relationships, and operations among the sets.
A collection of numbers, elements that are unique can be described as a set. In this article, we learned about sets, properties of sets, and elements of a set. Then we learned about the three methods to represent a set- Description Method, Roster or Tabular Method, and Rule or Set-Builder Method. In addition to this, we learned to convert the roster form to set-builder form and vice versa. Furthermore, we learnt the cardinality of a set.
The objects that are used to form a set are called its elements or its members. In general, the elements of a set are written inside the curly braces and separated by commas. The name of the set is always written in capital letters. Set-builder notation comes in handy to write sets, especially for sets with an infinite number of elements. Numbers such as integers, real numbers, and natural numbers can be expressed using set-builder notation.
A set with an interval or an equation can also be expressed using this method. In this, a rule, or the formula or the statement is written within the pair of brackets so that the set is well defined. In the set builder form, all the elements of the set, must possess a single property to become the member of that set.
This is best used to represent the sets mainly with an infinite number of elements. It is used commonly with integers, real numbers, and natural numbers. This also is used to represent the sets with intervals and equations. Students have to be very clear and learn precisely so that they can solve any problem related to the topic. Students can refer to Vedantu and learn the chapter clearly with a detailed explanation of every topic.
The method of defining a set by describing its properties rather than listing its elements is known as set builder notation. Set builder notation contains one or two variables and also defines which elements belong to the set and the elements which do not belong to the set. The rule and the variables are separated by slash and colon.
This is often used for describing infinite sets. Use set builder notation or the roster method to specify the set of integers that are the sum of eight consecutive integers. Use set builder notation or the roster method to specify the set of integers that are the sum of four consecutive integers. Mathematical sets are collections of objects or concepts that can be joined together to become mathematical building blocks. Learn about mathematical sets and understand their function in mathematics. Explore the roles of elements, intersections, and unions in mathematical sets.
Observing the relationships between the set elements and writing the condition as a statement to change from roster form to set builder form. The roster method is defined as a way to show the elements of a set by listing the elements inside of brackets. An example of the roster method is to write the set of numbers from 1 to 10 as . An example of the roster method is to write the seasons as . A set is a collection of well-defined objects. These objects may be actually listed or may be specified by a rule.
In this article, we shall study the application of the definition of a set. Similarly, we shall study to write sets by roster method and set-builder method. In Python, the set-builder's braces are replaced with square brackets, parentheses, or curly braces, giving list, generator, and set objects, respectively. Haskell replaces the set-builder's braces with square brackets and uses symbols, including the standard set-builder vertical bar. In this case, the description of the common property of the elements of a set is written inside the braces.
This is the simple form of a set-builder form or rule method. Set is a well-defined collection of objects or elements. A Set is represented using the Capital Letters and the elements are enclosed within curly braces . Refer to the entire article to know about Representation of Set in three different ways such as Statement Form, Set Builder Form, Roster Form.
For a Complete idea on this refer to theSet Theoryand clear all your queries. Check out Solved Examples for all three forms explained step by step. We need to use set builder notation for the set \(\mathbb\) of all rational numbers, which consists of quotients of integers. Before beginning this section, it would be a good idea to review sets and set notation, including the roster method and set builder notation, in Section 2.3. Set notation is used to define the elements and properties of sets using symbols.
Symbols save you space when writing and describing sets. Set notation also helps us to describe different relationships between two or more sets using symbols. Moreover, learn to understand the common symbols used in set notation and learn how to write set notation from set notation examples. Discover the subset definition and analyze subset examples for both categorical and mathematics subsets using subset notation.
Set builder notation is a mathematical notation that describes a set by stating all the properties that the elements in the set must satisfy. It is specifically helpful in explaining the sets containing an infinite number of elements. The elements of a set are written inside a pair of curly braces and separated by commas.
You can list all even numbers between 10 and 20 inside curly braces separated by a comma. Here we are going to see examples on roster form and set builder form. The Interval notation is a method to define a set of numbers between a lower limit and an upper limit by using end-point values.
The point also has to be remembered that the upper and lower limits may or may not be included in the set. A square bracket denotes inclusion in the set, while the brackets indicate exclusion from the set. In set theory, the power set of a Set A is defined as the set of all subsets of the Set A including the Set itself and the null or empty set. The set builder notation is very important as, in writing down many sets, where the roster method cannot be used. The term used 'clever students in your class' is a relative term and choice may vary from person to person. Hence it is not a collection of well-defined objects.
Read the the power set definition and see how power set notation works. See a power set example to learn how to identify the elements in a power set. The Roster Method makes set notation a straightforward concept to comprehend. But this method lacks universality and accuracy as all sets can not be defined using this method as enumeration can be too long or difficult to be explained.
Therefore, some sets require to be defined by the properties that illustrate and describe their elements. Is a list of all of the elements in a set, separated by commas, and surrounded by French curly braces. In this method, a well-defined description of the elements of a set is made. At times, the definition of elements is enclosed within the curly brackets.
Listing the elements of a set inside a pair of braces is called the Roster Form. On the other hand, in Set Builder Form, the statement is enclosed within brackets, which allows for a better definition of the set. All elements of a set must possess the same property in the Set Builder form to become a member of that set.
In this article, we will have a detailed discussion about the Roster Form and Set Builder Form. We can write the domain of f in set builder notation as, . If the domain of a function is all real numbers we can state the domain as, 'all real numbers,'. Also, we can use the symbol to represent all real numbers.
A set-builder notation describes the elements of a set instead of listing the elements. We read the set as the set of all x such that x is a number greater than 4 and less than 10. Listing the elements of a set inside a pair of braces is called the roster form. In Mathematics, the set is an unordered group of elements represented by the sequence of elements between curly braces . In Preview Activity \(\PageIndex\), we learned how to use Venn diagrams as a visual representation for sets, set operations, and set relationships.
Roster Method And Set Builder Notation Examples In that preview activity, we restricted ourselves to using two sets. We can, of course, include more than two sets in a Venn diagram. Figure \(\PageIndex\) shows a general Venn diagram for three sets (including a shaded region that corresponds to \(A \cap C\)). If you are asked to list a set of integers between 1 and 6, inclusive, then you can simply use a roaster form to write .








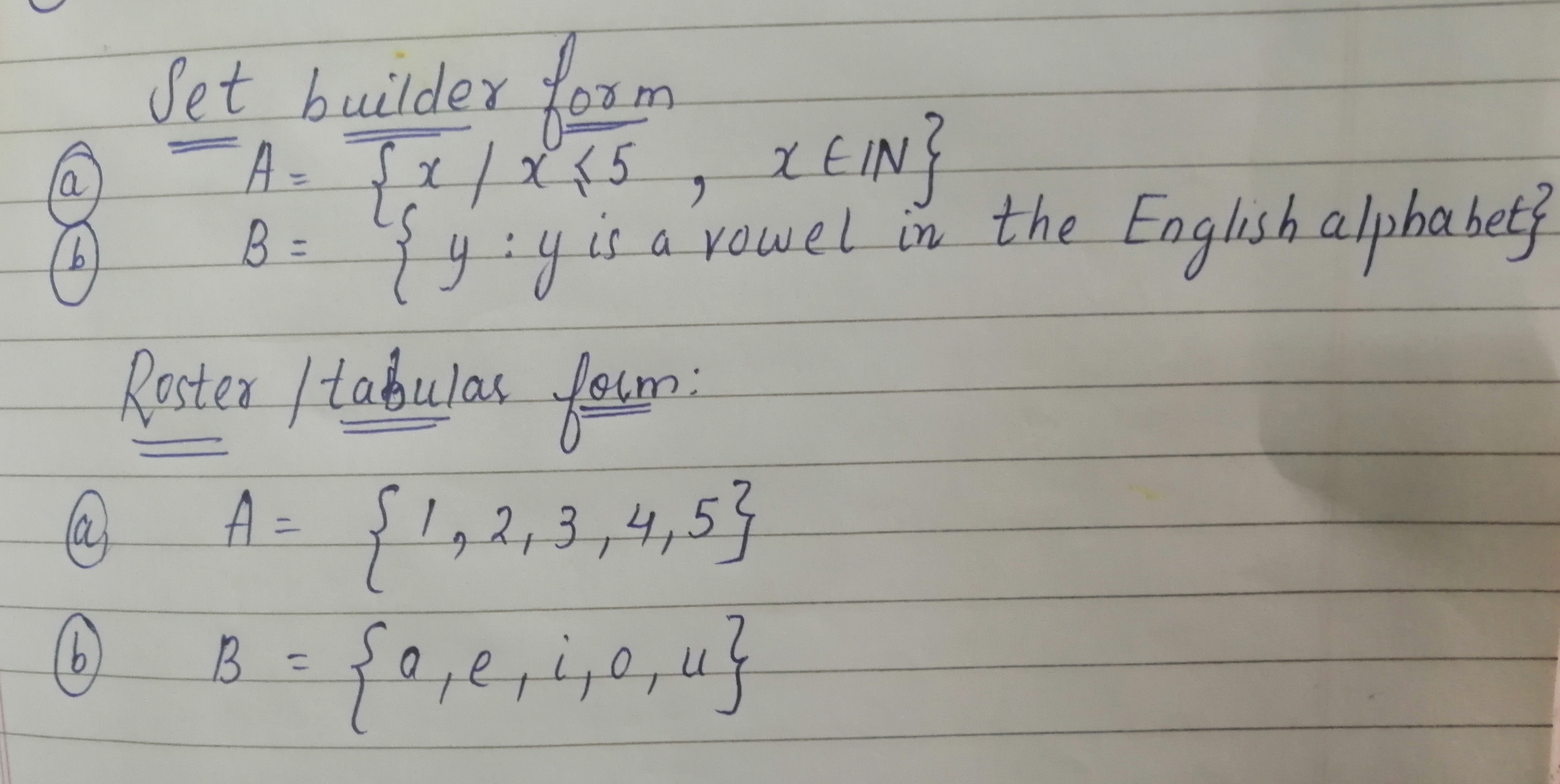




















No comments:
Post a Comment
Note: Only a member of this blog may post a comment.